Step-by-Step Noise Analysis Guide for Your Signal Chain

Abstract

This article presents the steps needed to carry out a theoretical analysis on the noise performance for a high speed wide bandwidth signal chain. Although a specific signal chain is chosen for the analysis, the steps highlighted can be considered valid for any type of signal chain. Five main phases are suggested: declaring the assumptions, drawing a simplified schematic of the chain signal, calculating the equivalent noise bandwidth for each of the signal chain blocks, calculating the noise contribution at the output of the signal chain for all blocks, and adding all noise contributions. The analysis shows how simple math can be used to describe all noise contributions. Gaining an understanding of how each block contributes to the overall noise allows the designer to appropriately modify the design (for example, choice of components) to optimize its noise performance.

Introduction

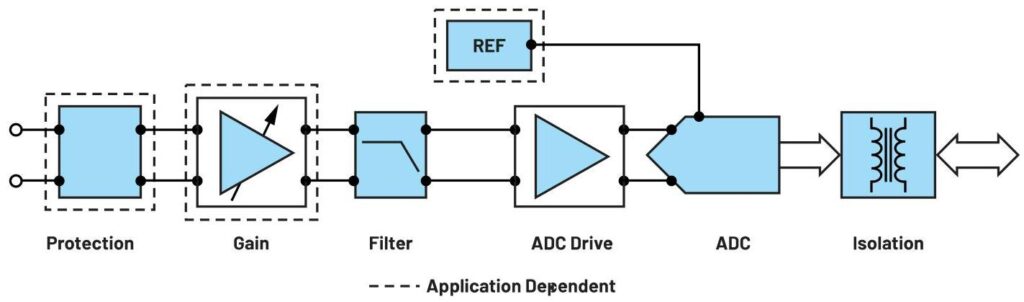
When designing a measurement signal chain, it is important to work through a noise analysis to determine if the signal chain solution will have low enough noise so that the smallest signal of interest can easily be extracted. A thorough noise analysis can save time and money during the production process. This article will outline the main steps necessary to carry out a signal chain noise analysis. We will use an example of the power optimized current and voltage measurement signal chain on the Analog Devices precision wide bandwidth technology page.

Current and voltage measurement

Signal chain options for measuring wide bandwidths up to 1 MHz for noise performance to support AC and/or DC analysis

Figure 1. A precision wide bandwidth current/voltage measurement power optimized signal chain.

The analysis is broken into five main steps:

1. Declaring assumptions
2. Drawing a simplified schematic of the chain signal
3. Calculating the equivalent noise bandwidth for each of the signal chain blocks
4. Calculating the noise contribution at the output of the signal chain for all blocks
5. Adding all noise contributions

1. Declaring Assumptions

For the noise analysis, or any analysis performed on a signal chain circuit, it is important to outline the assumptions made for each block in the signal chain. Outlined are some of the assumptions made for this work:

Protection block

• It is assumed that the protection block doesn’t add any significant noise. The noise from this block would be caused by the small on resistance of the protection switch block. In the following example we use the ADG5421F, which has an on resistance of 11 Ohm, and so generates a noise spectral density (NSD) of 0.43 nV/sqrt(Hz). As this value is 18 times smaller than the lowest NSD of the gain block, it does not need to be considered. If additional protection measures are implemented (TVS diodes, etc.), these would also need to be taken into consideration.

Signal filtering block

• It is assumed the signal filtering block has only one pole. Assuming a single pole is sufficient given the bandwidth that is being examined (400 kHz) vs. the sampling frequency (15 MSPS).

Reference block

• It is assumed that noise from the reference block is negligible as the voltage reference chosen has excellent noise performance (0.25 ppm p-p (10 Hz to 1 kHz) and 0.21 ppm rms (10 Hz to 1 kHz)) and therefore is not included in analysis. This is specific to this signal chain example, and further analysis would be necessary if a different signal chain and reference are used.^1

Isolation block

• Noise from the isolation block is not considered.

Additional assumptions

• The analysis is carried out at a temperature of 25 degC (298.15 K).
• The NSD of the given block is assumed to be uniform over the sampling frequency. Only thermal noise is considered.
• For the ADC, the overall noise is taken (both kTC and additional noise sources).
• The sampling frequency (15 MSPS) is much larger than the bandwidth that is being examined (400 kHz).

Figure 2. A simplified signal chain.

2. Drawing a Simplified Schematic of the Signal Chain

From the signal chain solution (see Figure 1) a simplified schematic is generated (see Figure 2) for each of the following stages:

• Gain block
• Signal filter
• ADC driver
• ADC input RC filter
• ADC

We can also note:

• The gain stage is treated as a black box since its noise performance is based on its gain and considers all internal noise sources. This means the noise generated in the gain stage can be calculated directly using the NSD value of the gain amplifier from the data sheet. The gain selection is fully contained within the gain stage.
• The signal filter is embedded within the driver. The choice of using a passive filter reduces the overall power, which is one of the main attributes of the signal chain under analysis. By doing this, the values of R_filter, R_G, and R_F need to be carefully chosen to ensure an overall signal gain of 1, as highlighted in Figure 4. The value of R_G contributes to the bandwidth of the signal filter as follows:

where

• The component values for the RC network stage, which occurs just before the ADC sampling, are found using the Precision ADC Driver Tool. The default values from this tool are used in the signal chain analysis calculations. These values may also be found on the product data sheet or calculated.^2

3. and 4. Calculating the Equivalent Noise Bandwidth (ENB) for Each of the Signal Chain Blocks and Calculating the Noise Contribution at the Output of the Signal Chain for All Blocks

In this section we will calculate the equivalent noise bandwidth and noise contribution of all blocks individually.

Key Formulas to Note:

• The NSD of the resistors can be found by:

• The equivalent noise bandwidth (ENB) is the bandwidth of a brick wall filter that produces the same integrated noise power as the implemented filter.^3

• The ENB for the signal chain blocks is calculated by:

For a single-pole system:

For the ADC input RC filter (2-pole system):

Note: this formula is only suitable for the combination of a 2-pole filter generated by this ADC input RC filter and ADC sampling RC network. When using different filter combinations there may be different considerations required.

• For systems with two or more poles, see Table 1. The noise bandwidth ratio is used in calculating the ENB.^3

(1.57 = pi/2)

Table 1. Noise Bandwidth Ratio vs. Poles

The following analysis applies when a passive filter is used for the signal filter, as shown in Figure 3.

Note: For this analysis in the signal filter R_filter = R_G = R_driver / 2.

This is done to avoid gain at the driver stage, as we only want gain to occur in the gain block. Also R_driver = R_F as shown in Figure 4.

Gain Block

• Noise produced by the gain block is filtered by the filter block, which has much lower bandwidth than the filter generated by the ADC drive output RC network and the ADC input sampling network.

• ENB = bandwidth x pi / 2

• noise_gain_stage = NSD x PGA_gain x sqrt(ENB)

• The NSD value considers all the noise sources of the gain block and is given in the data sheet.

Figure 3. Schematic sections for noise analysis.

Figure 4. Setting resistor values for noise analysis.

For Signal Filter

• The signal filter or antialiasing filter should be designed to maintain a gain of 1 in the fully differential amplifier (FDA) stage that comes next in the chain. This will mean splitting the FDA input resistor into two equal resistors — one used in the passive signal filter and the other used on the input of the FDA:

Noise generated by the filter resistors (R_filter) is filtered by the filter itself, which has much lower bandwidth than the combined filter generated by the ADC input RC filter and the ADC sampling RC.

• ENB = (bandwidth x pi) / 2

• noise_signal_filter = sqrt(2 x 4 x k x T x (R_driver / 2) x ENB) [V rms]

• The 2 is related to the differential scheme.

For ADC Driver Amp Resistors

• Noise generated by the amplifier resistors (R_driver and R_driver/2 highlighted in Figure 4) is filtered by the combined filter that exists in the next two blocks of the signal chain.

• This is a second-order filter consisting of the ADC input RC filter and the ADC sampling RC.

• ENB = 1.22 / (2 x pi x R_ADC_filter x (C_ADC_filter + C_ADC_sampling))

• noise_driver_amp_input_resistors = sqrt(2 x 4 x 4 x k x T x R_driver/2 x ENB) [V rms]

• The 2 is related to the differential scheme.

• The 4 is related to the noise gain: (R_driver / (R_driver/2))^2 = 2^2

• noise_driver_amp_feedback_resistors = sqrt(2 x 4 x k x T x R_driver x ENB) [V rms]

• The 2 is related to the differential scheme.

These are combined in the same step as follows:

• noise_driver_amp_resistors = sqrt((2 x 4 x k x T x R_driver/2 x ENB) + (2 x 4 x k x T x R_driver x ENB))

For Driver Amp

• Noise generated by the amplifier driver is filtered by the combined filter generated by the ADC input RC filter and the ADC sampling RC.

• Second-order filter

• ENB = 1.22 / (2 x pi x R_ADC_filter x (C_ADC_filter + C_ADC_sampling))

• noise_driver_amp = NSD_driver x sqrt(9 x ENB) [V rms]

• The 9 is related to the amplifier noise gain: (1 + R_driver / (R_driver/2))^2 = 3^2

ADC Input RC Filter

• Noise generated by the resistor in the ADC input RC filter network is filtered by the combined filter generated by the ADC input RC filter and the ADC sampling RC.

• Second-order filter

• ENB = 1.22 / (2 x pi x R_ADC_filter x (C_ADC_filter + C_ADC_sampling))
• noise_ADC_input_RC_filter = sqrt(2 x 4 x k x T x R_ADC_input_filter x ENB) [V rms]
• The 2 is related to the differential scheme.

ADC

• Noise generated by the ADC can be directly added and calculated from the data sheet.

• Full-scale amplitude and signal-to-noise ratio (SNR) in units of dBFS can be found from the data sheet.

5. Calculating the Noise of the Signal Chain

• To add all the noise contributions, the root sum square method is used:

Noise Spectral Density

• Noise spectral density (NSD) can be calculated considering the ADC sampling frequency.

Key Points to Note

• NSD on different parts can only be added directly if they are measured over the same bandwidth.
• The choice of the signal filter resistor values depends on the application requirements of noise vs. power consumption of your signal chain and the bandwidth being examined.

For further I&V noise, bandwidth, and power analysis:

Summary Sheet

Figure 5. Summary sheet.

Table 2. Individual Noise Sources of a Differential Signal Chain

Figure 6. Worked example.

Table 3. Noise Contribution of the Different Stages from the Example in Figure 6

*Above measurements are all uV rms

R_filter = R_G = R_driver/2 = 250 Ohm, R_driver = R_F = 500 Ohm, R_ADC_filter = 25 Ohm

Conclusion

By following these steps, the designer will be able to analyze and calculate the noise performance of the chosen signal chain. The analysis provides useful insights on how different components in the signal chain affect the noise performance and how these could be minimized (for example, changing resistors‘ size, changing a component, or minimizing equivalent noise bandwidths). Therefore, the designer can create a proposal that ensures the signal chain extracts the smallest signal of interest, which helps save time and money.

Appendix

Other Configurations:

There is an option of using an active filter instead of a passive filter, as shown in Figure 7.

Choosing whether to use an active or passive filter in the signal chain will depend on the applications. The active filter used in the analysis had low current consumption and low noise. However, it may be unsuitable for some applications as its distortion performance is not as good over frequency.

If the active filter is chosen, it is necessary to make changes to the calculations:

For Signal Filter

• ENB = bandwidth x pi / 2

Active filter:

• noise_active_filter = sqrt(2 x 4 x k x T x R_filter x ENB) [V rms]

• The 2 is related to the differential scheme.

• R_filter is chosen to maintain a gain of 1.

For Filter Amp

When the active filter version is used there is noise from the filter amp, which forms part of the active filter. This is not necessary for use with the passive filter circuit as no filter amp is used.

• ENB = 1.22 / (2 x pi x R_ADC_filter x (C_ADC_filter + C_ADC_sampling))
• noise_filter_amp = NSD x sqrt(2 x ENB) [V rms]

For ADC Driver Amp Resistors

• ENB = 1.22 / (2 x pi x R_ADC_filter x (C_ADC_filter + C_ADC_sampling))

Active filter:

• noise_driver_amp_input_resistor = sqrt(2 x 1 x 4 x k x T x R_driver x ENB) [V rms]

• The 2 is related to the differential scheme.

• Note: the noise gain at the amp driver in the active filter circuit is 1: (R_driver / R_driver)^2 = 1^2

• noise_driver_amp_feedback_resistor = sqrt(2 x 4 x k x T x R_driver x ENB) [V rms]

• The 2 is related to the differential scheme.

These are combined as follows:

• noise_driver_amp_resistor = sqrt(4 x 4 x k x T x R_driver x ENB) [V rms]

For Driver Amp

• ENB = 1.22 / (2 x pi x R_ADC_filter x (C_ADC_filter + C_ADC_sampling))

Active filter:

• noise_driver_amp = NSD_driver x sqrt(4 x ENB) [V rms]

• The 4 is related to the amplifier noise gain: (1 + R_driver / R_driver)^2 = 2^2

This is specific to the amplifier driver being used.

• Here we can use the single-ended equivalent circuit with all its noise appearing at the positive input of the op amp.

All other calculations remain as described.

Figure 7. Active filter configuration.

References

1. Alan Walsh. „Voltage Reference Design for Precision Successive-Approximation ADCs.“ Analog Dialogue, Vol. 47, No. 2, June 2013.
2. Alan Walsh. „Front-End Amplifier and RC Filter Design for a Precision SAR Analog-to-Digital Converter.“ Analog Dialogue, Vol. 46, No. 4, December 2012.
3. Tim J. Sobering. „Technote 1: Equivalent Noise Bandwidth.“ Kansas State University. May 1991. „MT-048 Tutorial: Op Amp Noise Relationships: 1/f Noise, RMS Noise, and Equivalent Noise Bandwidth.“ Analog Devices, Inc., 2009.

About the Authors

Pasquale Delizia: Pasquale Delizia received a master’s degree in electronic engineering from the Polytechnic University of Bari, Italy, in 2006 and a Ph.D. degree in microelectronics from the University of Lecce, Italy, in 2010. He was awarded an M.B.A. from the Henley Business School, University of Reading, in 2021. Since 2010, he has been part of the Precision Converter Technology Group at Analog Devices. After working on precision converter architectures, he transitioned into a marketing role within the same group. He can be reached at .

Rose Delaney: Rose Delaney is an electrical and electronics engineering undergraduate student at University College Cork, Ireland. She joined Analog Devices as a product applications co-op student in 2021 in the Precision Technology Group.